解决问题的流程称为算法, 数据结构是这个过程中的一环
仅总结, 不分析, 通过学习别人制造体系, 收集遇到的来丰富

收集:

• OI wiki
• wikipedia, 深入了解直接搜, 超详细, 引用也很有用, 但是中文版没有英文版详细

数据结构

学习流程:

1. 结构定义
   tutorialspoint
2. 基本操作方法, 一般与上方在一块
3. 学习(读懂)
   语言: python
4. 考察, online judge problem set
   LeetCode
   Geeksforgeek
5. 经典应用与cs方面的应用, serach google
   application of xxx / real life use of xxx
6. 将来碰到了有趣的应用也会收集在这

最基本的考察: 创建, 展示(遍历), 插入, 删除, 查询, 更改。所以不会再包含

如何读懂: 提取核心算法, 使用实际数据脑中执行一遍, 作图辅助, 熟悉相关基础

与内存直接挂钩的数据结构和抽象使用的数据结构

链表

1. Simple Linked List
2. Doubly Linked List
3. Circular Linked List
4. Circular Doubly Linked List
5. 跳跃表

考察:

1. 链表反转

链表的应用:

in computer science

1. 可以实现堆栈与队列
2. 实现邻接图
3. [跳跃表]二分搜索

in real world

1. image viewer - 前进和后退
2. music player

Applications of linked list data structure

堆栈和队列

1. stack
2. queue
3. 单调栈
4. 优先队列

cs

1. prefix, postfix notation (波兰表达式)
   中缀适合人类读
2. syntax parsing
3. backtracking, 图的搜索
4. function call
5. [单调栈] 查询区间最值, 第k个xxx, 出现于动规
6. [stack] DFS, [queue] BFS

Applications of Stack

real

1. undo/redo operation
2. 缓冲区

树

1. tree
2. Binary Search Tree
3. AVL Tree
4. Spanning Tree 生成树
5. Heap

考察:

1. 遍历, 前中后
2. 树的高度
3. AVL平衡旋转

cs

1. Minimum Spanning-Tree Algorithm => Kruskal and Prim
2. Heap sort
3. [Heap] prior queue

real

1. [spanning Tree] 路由协议

图

1. 邻接矩阵
2. 邻接表

考察:

1. 深度优先
2. 广度优先
3. 最短路径 - Dijkstra, Floyd

cs

1. database ER diagram

real

1. route

哈希表

1. 哈希数组

考察:

1. 哈希碰撞 - 线性检测, Separate chaining

cs

1. 对象, HashMap in java, dict in python, js 的 object 在v8 里不是 hash, 是由静态类生成的 - How does JavaScript VM implements Object property access? Is it Hashtable?

算法

流程: 设计, 分析, 实现, 试验, 改进

设计: 选用 DS, 算法
实现: 使用语言特性
改进: 根据性能和 debug 改善代码

算法可以归类为: DS相关 (如上), 应用场景 (排序, 字符串, 图, 查找), 设计方法 (动规, 贪心, 回溯, 分治, 枚举)

学习流程:

1. 针对问题场景
2. 基本流程和时间空间复杂度 - 部分添加参考引用
3. 将自己的理解输出, 编程实现, 再学习最佳实践
4. 考察, 总结使用这个算法的问题的特点

原始算法存在多个改进版本, 这里并不会介绍, 但是如果有需要会将来另开篇文章总结

算法与内存, cpu

1. 根据 cpu 缓存命中算法, 取数据尽量是在一块 - 堆排序
2. 数组在内存中是一块连续的空间, 如果过大, 很难找到

   如何衡量

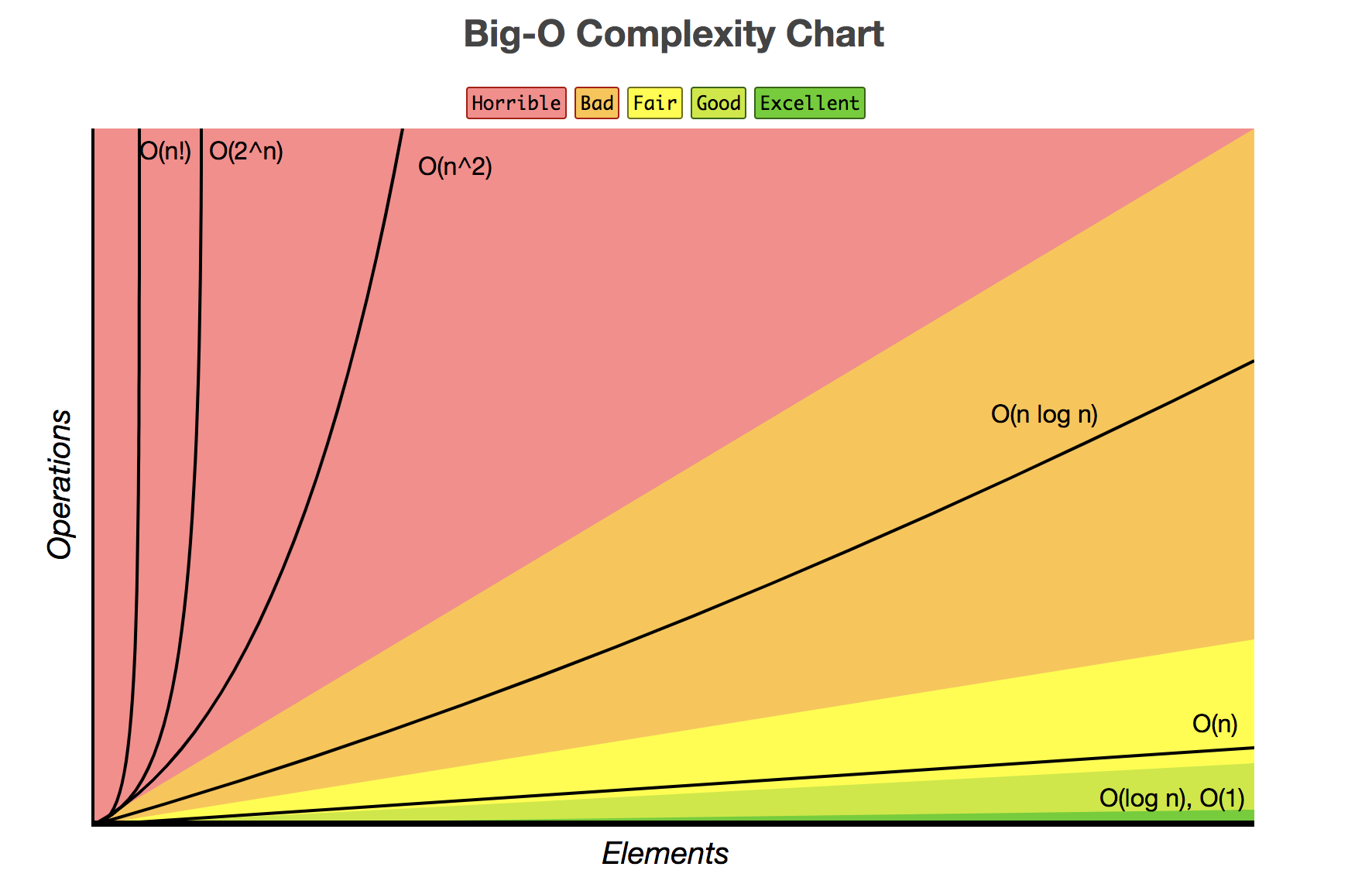
时间复杂度分析:

• 渐近符号记法: 考察输入值大小趋近无穷, 不包括这个函数的低阶项和首项系数
  O: 运行时间的渐近上界
  Ω: 运行时间的渐近下界
  Θ: 运行时间的渐近确界

  算法时间复杂度用 O 表示, 最坏不会超过 (不研究了, 反正也没什么大用)

• 问题规模: 输入数据的大小 n
  时间复杂度: T(n)=O(f(n)), f(n)=2n^2+1^,O(f(n))=O(n^2^)
• 主定理: 奠定算法分析尤其是递归算法的理论基石

  根据递推关系式中的f(n)来推导时间复杂度T(n)
  主定理
  用主定理搞事情

从代码计算时间复杂度 - 根据代码中的循环操作转换为变量为 n 的函数

从设计计算时间复杂度 - 分成步骤, 合并步骤中每个元素执行次数

算法与数据结构之间的比较
常见算法复杂度Cheatsheet

排序

原地: 排序时只有常数个元素需要存储在数组之外
稳定: 排序后不改变相同数值的相关位置
自适应: 排序时不再排序原数组中已经排序好的部分
基于比较: 排序时通过比较大小来进行操作

通过交换相邻元素来进行排序的任何算法都需要Ο(n²)的时间, 因为一次最多只能消除一个逆序,
O(nlogn)是基于比较的排序算法的时间复杂度下界
高效排序算法——希尔排序、堆排序、归并排序、快速排序
Sorting algorithm

最差时间 Ο(n²)

1. 冒泡 - 原地, 基于比较
2. 插入 - 原地, 基于比较
3. 选择 - 原地, 基于比较

插入排序可以避免已经排序好的数组再次重新比较 (最佳O(n)), 但是每一次交换都需要三次赋值操作, 所以反而会比选择排序耗费时间更长 - 插入排序与选择排序的比较

最差时间 Ο(n log n)

没有基于比较的排序算法能比其快, 只有依赖输入为特殊性质的排序算法能超过它们

1.归并 - 基于分治技术
可以使用多个 cpu 来执行

递归划分数组 - logn, 2^k = n
数组排序 - n, 利用已排序好的性质通过比较放入额外创建的数组中
合并一下: n*(logn + 1/2logn + …) <= 2nlogn

2. 快排

由冒泡排序进行改进

选取pivot划分数组 - 假设每次都选的好正好分一半, logn, 选得不好比如说正好是逆序, 那么就会是 n
排序 - 一遍循环, 将大于pivot和小于pivot的调换位置, 直到两个指针相遇, n
合并的话就是 nlogn, 当然对于这些典型的递归算法也可以用主定理来解 - wiki-快速排序

没有优化重复元素(三向切分快排)比不过希尔排序、堆排序和归并排序

3. 堆
   提升版的选择排序, 在实际运行时, 由于计算机cpu缓存命中的缘故不如提升版的快排(局部性)

将数组转换为堆 - n
循环取出第一个元素并维护优先队列 - nlogn, 维护的时间复杂度为 logn
合并: n + nlogn => nlogn
Heapsort
为什么在平均情况下快速排序比堆排序要优秀？

在语言内部的排序算法中, 会根据数组的长度等信息选择不同的排序算法, 一般来说经过多重优化, 比自己实现的效率会高不少

杂项

基数, 希尔, 桶

1. 希尔 - 基于插入排序, 最优可达n^4/3

第一批冲破 o(n²) 的算法。选择希尔增量依照最原始为n/2, 按照大小将数组分组, 每组进行插入排序, 将增量依次除2并排序直到1, 最后一次执行完插入排序后, 此时数组有序

依照希尔序列划分数组: logn
每次进行插入排序: 最好 - n, 最坏 - n², 因为每次都将较远的逆序对消除, 不会有最坏出现 - 由于希尔排序数学分析较难, 这里没有给出合并
希尔排序为什么会那么牛那么快，能够证明吗？
图解排序算法(二)之希尔排序

查找

二分

基于分治思想, 在有序数组上执行

将数组不断中值划分比较 - logn
在求 mid 索引的时候, 为了避免数组超过 int 范围, 使用这种写法: mid = low + (high - low) / 2

插值

在二分的方法上改进过来的, 只不过二分猜测值的位置在中间, 插值猜测值的位置由插值公式给出, 公式:

left + parseInt(( key - data[left] ) / ( data[right] - data[left] ))*( right - left )

复杂度为o(log(logn)), 可以看看这个 paper, 对目前的我没什么大用, 姑且留个记号

哈希表

根据哈希数据结构而来, 时间复杂度为 O(1)

字符串

// TODO 2020.3 之前

数组

双指针

shuffle 洗牌